Find the center and radius of the circle. Then graph the circle.
x2 + y2 + 4y – 45 = 0
Solution:-
To find the center and the radius, you must complete the square and then write the equation in standard form.
(x – h)2 + (y – k)2 = r2
Regroup the terms.
(x2) + (y2 + 4y) – 45 = 0
Since x is square, there is nothing needed.
Now complete the square for y2 + 4y.
To complete the square, add and subtract 4 inside the second set of parentheses.
x2 + (y2 + 4y + 4 – 4 ) – 45 = 0
Now remove the subtract term from within the parentheses.
x2 + (y2 + 4y + 4 – 4 ) – 45 = 0
Use the addition principle to get the constant terms on the right side of the equation.
x2 + (y2 + 4y + 4 ) = 49
Now writ the equation in standard form.
(x -h)2 + (y – k)2 = r2
(x – 0)2 + (y + 2)2 = 49
h = 0
k = -2
The radius is 7.
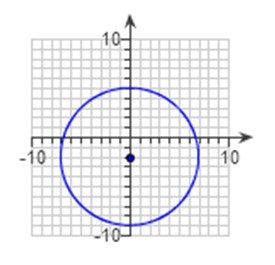
To sum up, the center is (0, -2) and the radius is 7.
To graph the circle, first plot the center (0,-2).
To complete the circle, use the radius to find all the point equidistant from the center.