Problem 1117

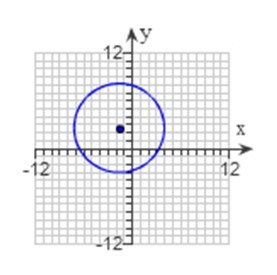
Find the center and radius of the circle. Then graph the circle.

x² + y² + 3x – 5y – $\frac{91}{4}$ = 0

Solution:-

To find the center and the radius, complete the square and then write the equation in standard form.

(x – h)² + (y – k)² = r

Regroup the terms.

(x² + 3x ) + (y² – 5y) = $\frac{91}{4}$

First complete the square, add $\frac{9}{4}$ to both sides of the equation.

(x² + 3x + $\frac{9}{4}$ ) + (y² -5y) = $\frac{91}{4} + \frac{9}{4}$

Now complete square for y² – 5y.

To complete the square, add $\frac{25}{4}$ to both sides of the equation.

(x + 3x + $\frac{9}{4}$ ) + (y – 5y + $\frac{25}{4}$ )

= $\frac{91}{4}+\frac{9}{4}+\frac{25}{4}$

Simplify the right-hand side.

(x + 3x + $\frac{9}{4}$ ) + (y – 5y + $\frac{25}{4}$ )= $\frac{125}{4}$

Now write the equation in standard form.

(x – h)² + (y – k)² = r²

$(x+\frac{3}{2})^{2}+(y-\frac{5}{2})^{2}=\frac{125}{4}$

h = – $\frac{3}{2}$

k = $\frac{5}{2}$

The radius is $\frac{5\sqrt{5}}{2}$ .

To sum up, the center is ( $-\frac{3}{2},\frac{5}{2}$ ) and the radius is $\frac{5\sqrt{5}}{2}$ .

To graph the circle, first plot the center (- $\frac{3}{2},\frac{5}{2}$ ).

To complete the circle, use the radius to find all the points equidistant from the center.