Problem 891

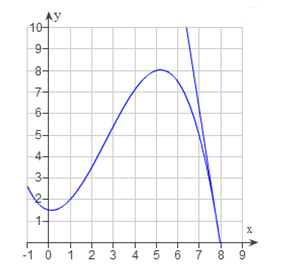
Estimate the slope (in y-units per x-unit) of the tangent line to the curve.

 

Solution:-

 

First look at the tangent line on the curve.

When moving from left to right the line decreases.

Therefore the slope of the line will be negative.

The slope of a line L is defined as

sloe =

where (x,y) and are points on the line.

To estimate the slope, start at any point on the line and move one unit to the right on the x-axis. Estimate the new value y_o of the line at x = x_o + 1. The slope will be the difference y – y₀.

If we start at x_o = 7 we can estimate that y₀ 6.

Now we move 1 unit to the right on the x-axis to x = 8.

At x = 8 we estimate that y 0.

Therefore,

slope