The birth weights of full-term babies are normally distributed with mean 3800 grams and standard deviation σ = 470 grams. Use this information to do the following.
(a)Draw a normal curve with the parameters labeled.
(b)Shaded the region that represents the proportion of full-term babies who weigh more than 4740 grams.
(c) Suppose the area under the normal curve to the right of X = 4740 is 0.0228. Provide an interpretation of this result.
Solution:-
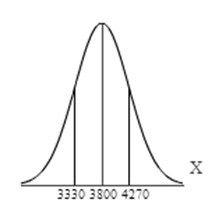
(a ) The graph of a normal curve is symmetric about the mean, µ, and has inflection points at µ ± σ.
Determine the location of the inflection points.
µ – σ = 38000 – 470 = 3330
µ +σ = 3800 + 470 = 4270
The graph that is symmetrical about 3800 and has inflection points at 3330 and 4270 is shown to the right.
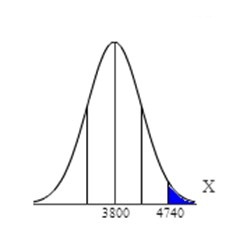
(b) Shade the region that represents the proportion of full-term babies who weigh more than 4710 grams.
For the given normal distribution curve, the area under the curve to the left of a value shows the percentage of births that weigh less than that value, and the area under the curve to the right of a value shows the percentage of births that weigh more than that value.
Since we wish to shade the region that shown the full-term babies that weigh more than 4740 grams, we need to shade to the right of 4740.
The graph that shown the region to the right of 4740 shaded is shown to the right. Notice that 4740 is two standard deviations away from the mean.
(c ) Suppose the area under the normal curve to the right of X = 4740 is 0.0228. Provide an interpretation of this result.
Remember that for the given normal distribution curve, the area under to the left of a value shows the percentage of births that weigh less than that value, and the area under the curve to the right of a value shows the percentage of births that weigh more than that value.
Since the area under the normal curve to the right of X = 4710 represents the percentage of full-term babies that weigh more than 4740 grams. 2.28% of full-term babies weigh more than 4740 grams, or the probability is 0.0228 that a randomly selected full-term baby weighs more than 4740 grams.