Find the slope of a line given two points on the line
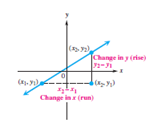
To obtain a formal definition of the slope of a line, we designate two different points on the line. To differentiate between the points, we write them as (x1 , y1) and (x2 , y2). See Figure (The small numbers 1 and 2 in these ordered pairs are called subscripts. Read (x1, y1) as “x-sub-one, y-sub-one.”) (x1, y1) and (x2, y2).
As we move along the line in Figure from (x1, y1) to (x2, y2), the y-value changes (vertically) from y1 to y2, an amount equal to y2 – y1. As y changes from y1 to y2, the value of x changes (horizontally) from x1 to x2 by the amount x2 – x1. The ratio of the change in y to the change in x (the rise over the run) is called the slope of the line, with the letter m traditionally used for slope.
Slope Formula
The slope of the line through the distinct points (x1, y1) and (x2, y2) is
![]() (x1 ≠ x2).
(x1 ≠ x2).